在一个传统设计中，你会发现在模数转换器 (ADC) 的前面有一个抗混叠滤波器。设计人员的解释是这么做符合那奎斯特定理，的确如此。ADC之前的滤波器减少了带外噪声，并且减弱了那些会被混叠回馈到信号链中的信号。

这一切都很平常。但是，一个未经证明的意外情况就是拐点频率，或者说-3dB频率 (f-3dB) 之前的模拟滤波器所带来的影响。直觉告诉我们这个滤波器在f-3dB频率上不会像矩形滤波器那样开始运行。但是，滤波器从f-3dB向DC移动时所导致的增益误差水平是多少呢（图1）？让我们来看一看这个评估中的Butterworth响应。

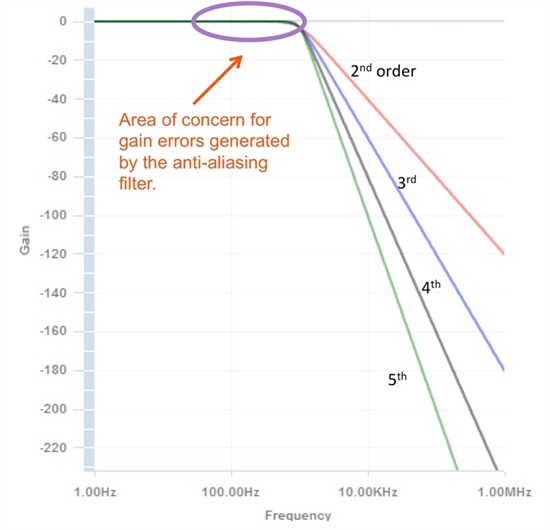
图1. 在f-3dB等于1kHz时，Butterworth低通滤波器响应

在输入频率带宽范围内，一个ADC的增益误差是静态的。例如，使用ADS8364时，一个典型16位ADC增益误差技术规格最大值可以是+/-0.25%FS。这等于164最低有效位 (LSB) 的满量程 (FS) 上的增益误差。这看起来似乎很高，但是可以对这个误差，连同转换器的偏移误差进行校准。

而在增加滤波器的模拟增益误差时，情况就不是这样了。低通滤波器的感应增益误差是由频率决定的。图2显示的是一个2^nd阶，Butterworth，低通滤波器的滤波器响应。

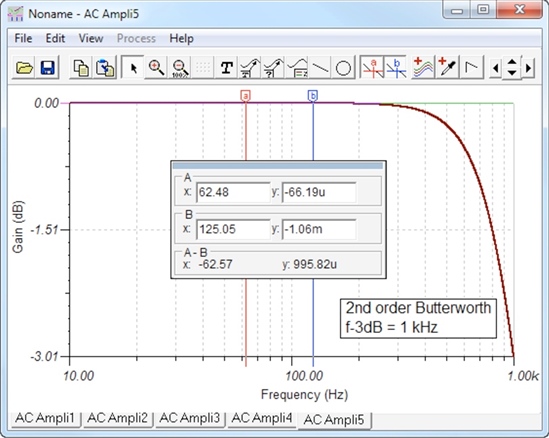
图2. 一个2^nd 阶，1kHz Butterworth Sallen-key有源滤波器的频率响应。这个仿真使用理想组件。

探针（a-红色）图示了16位转换器遇到半LSB增益误差时的频率。此处出现增益误差的频率为62.48Hz，对可用频率范围的减少超过了十倍频。对于一个12位转换器（探针b-蓝色），增益误差开始的频率（半LSB）大约为125Hz。在高于这个频率时，增益误差持续增加，直到这个滤波器的f-3dB。

当你增加滤波器的阶数时，这一情况会有所改进。图3显示的是5^th 阶，Butterworth滤波器的频率响应。

图3. 一个5^th 阶，1kHz Butterworth Sallen-key有源滤波器的频率响应。这个仿真使用理想组件。

与图2相比，图3中的情况已有所改进。对于16位转换器，半LSB误差开始于大约369Hz（a-红色），而对于12位滤波器开始于大约443Hz（b-蓝色）。

虽然我已经为你显示了Butterworth低通滤波器的工作方式，但这个现象在所有低通滤波器中都会出现—不论它们的拓扑是怎样的；essel、Chebyshev、线性相位、高斯，还有很多其它低通滤波器都是如此。此外，我们的示例是理想状态下的滤波器，其中的电阻器、电容器和放大器的运行方式都尽可能地接近计算得出的理想工作方式。非理想电容器和电阻器对于滤波器的频率响应虽然影响较小，但是不建议忽略掉这些很小的变化所带来的影响。

如果你想进一步研究这个运行方式，我建议你使用WEBENCH滤波器设计工具。其中有一个功能能够使你将整个滤波器设计导出到TINA-TI模型中进行进一步的仿真。请使用这一功能。这个功能将使你能够快速确认和验证你的滤波器设计。

参考文献

1. 模拟滤波器和技术规格畅游：选择正确的转换率，Baker Bonnie，与Bonnie一起研究电路板，08/27/14
2. 模拟滤波器和技术规格畅游：什么，我以为我已经除掉噪声了？Baker Bonnie，与Bonnie一起研究电路板，11/21/2013
3. 模拟滤波器和技术规格畅游：输入偏置电流大有用途，Baker Bonnie，与Bonnie一起研究电路板，11/21/13
4. 模拟滤波器和技术规格畅游：为你的滤波器选择正确的带宽，Baker Bonnie，与Bonnie一起研究电路板，11/08/13

*博客内容为网友个人发布，仅代表博主个人观点，如有侵权请联系工作人员删除。